티스토리 뷰
파스칼의 삼각형은 수학에서 이항계수를 삼각형 모양의 기하학적 형태로 배열한 것이다.
삼각형의 행의 수가 입력으로 주어졌을 때 파스칼의 삼각형을 출력하라.
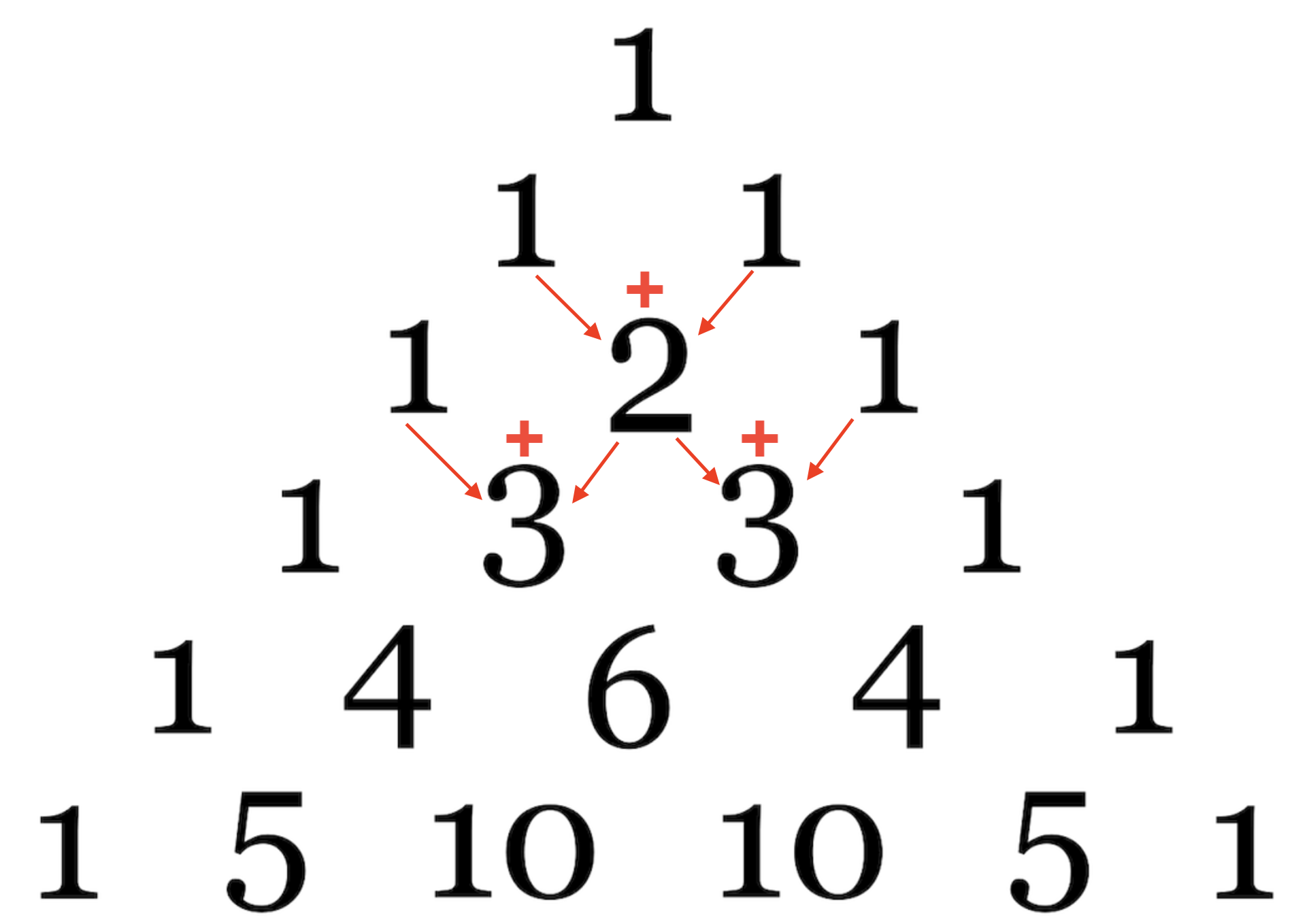
-
숫자가 들어갈 칸을 첫 번째 줄에는 1개, 두 번째 줄에는 2개, 세 번째 줄에는 3개 이런 식으로 한 줄씩 내려가면 한 칸씩 늘어나게 정삼각형 모양으로 만든다.
-
첫 번째 줄과 두 번째 줄의 3칸에는 1을 쓴다.
-
세 번째 줄부터는 줄의 양쪽 끝 칸에는 1을 쓰고 나머지 칸에는 바로 윗줄에 위치한 칸 중 해당 칸과 인접해 있는 두 칸의 숫자를 더해서 그 값을 쓴다.
- 출처 나무위키 -
파스칼 삼각형을 ArrayList 로 구현하였다.
삼각형의 한 행을 ArrayList 로 만든 다음 result 라는 ArrayList 에 넣어주었다.
ArrayList 안에 ArrayList 가 있는 형식이다.
파스칼 삼각형의 한 행을 구현 하기 위해서는 이전 행의 값을 가져와야 하며, 이전행의 현재 열과 이전 열의 값을 가져와서 더해서 만들어진다.
int data1 = result.get(i-1).get(j-1);
int data2 = result.get(i-1).get(j);
a.add(data1+data2);
이때 주의 해야할 점은 삼각형의 한행의 시작과 끝은 1이 되어야 한다.
이때 continue 를 사용한 이유는 행의 첫 시작인 j=0 일때는 리스트에 1이 add 되고 밑의 연산을 거치지 않기 위함이다.
j==i 일때는 행의 맨 끝이라 더 이상 연산을 하지 말라는 의미로 break 를 사용해도 되지만, break 를 사용하기 위해서는 또 다른 if 문이 필요하고 코드 줄이 길어져 한개의 if 문을 사용하기 위해 continue 를 사용하였다.
이때 for 문의 조건이 false 가 되 반복문이 종료가 된다.
if(j==0 || j == i){
a.add(j,1);
continue;
}
import java.util.ArrayList;
import java.util.Arrays;
public class Pascal {
public static ArrayList<ArrayList<Integer>> solution(int numRows) {
ArrayList<ArrayList<Integer>> result = new ArrayList();
for(int i=0; i < numRows; i++){
ArrayList a = new ArrayList<>();
for (int j = 0; j <= i; j++) {
if(j==0 || j == i){
a.add(j,1);
continue;
}
int data1 = result.get(i-1).get(j-1);
int data2 = result.get(i-1).get(j);
a.add(data1+data2);
}
result.add(a);
}
return result;
}
public static void main(String[] args) {
// Test code
System.out.println(solution(1));
System.out.println(solution(2));
System.out.println(solution(3));
System.out.println(solution(4));
System.out.println(solution(5));
}
}
코드를 다 작성하고 나서 간단하게 2차원 배열을 통해서 구현해도 될것 같다는 생각이 들었다.
아직 list 사용이 미숙하여 list 사용법을 익숙하기 위해서 ArrayList 를 사용하였다.
또한 ArrayList 에서 get 을 사용하면 Object 형으로 value 값을 가져오게 되는때 ArrayList 선언시에 ArrayList<Integer> 를 해주면 int 형으로 return 이 되어 쉽게 연산을 할 수 있다는 것을 깨달았다.
'Algorithm > 자료구조' 카테고리의 다른 글
| 자료구조 - 연결 리스트 Linked List (0) | 2022.11.22 |
|---|---|
| Catalan Numbers (0) | 2022.11.15 |
| 행복한 수 찾기 (수열) (0) | 2022.11.12 |
| 최대 공약수, 최소 공배수 구하기 (JAVA) (0) | 2022.11.09 |
| 경우의 수 구하기 (합의 법칙, 곱의 법칙) (0) | 2022.11.09 |
- Total
- Today
- Yesterday
- 취준
- 백준
- 자바
- 개발자 취준
- 제로베이스 백엔드 스쿨
- 코테공부
- 코테준비
- 프로그래머스
- 알고리즘
- 개발자 취업 준비
- 제로베이스 백준 장학금
- 코테 준비
- 코딩테스트 공부
- 코딩테스트공부
- 프로그래머스 자바
- 알고리즘공부
- 알고리즘 공부
- 취업 준비
- 개발자 면접 준비
- 취업준비
- 프로그래머스 카카오
- 코딩테스트 준비
- 코딩테스트
- 자바공부
- 주니어 개발자 취업 준비
- 백엔드 개발자
- java
- 기술 면접 준비
- 백엔드 개발자 기술 면접 준비
- 백엔드 개발자 취업 준비
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
